Drehzahl und Tragfähigkeit sind entscheidende Faktoren bei der Leistungsberechnung eines Kugellagers.
GMN entwickelt Kugellager für höchste Drehzahlen und maximale Belastung, um Effizienz und Lebensdauer von Maschinen zu optimieren. Eine entscheidende Größe stellt dabei die Drehzahlgrenze der Lager dar. Im Bereich der Kontaktflächen zwischen den Kugeln und den Ringen erhöht sich mit der Drehzahl progressiv die Laufreibung und somit die Lagertemperatur.
Die im Lager erzeugte Reibung wird entscheidend beeinflusst durch:
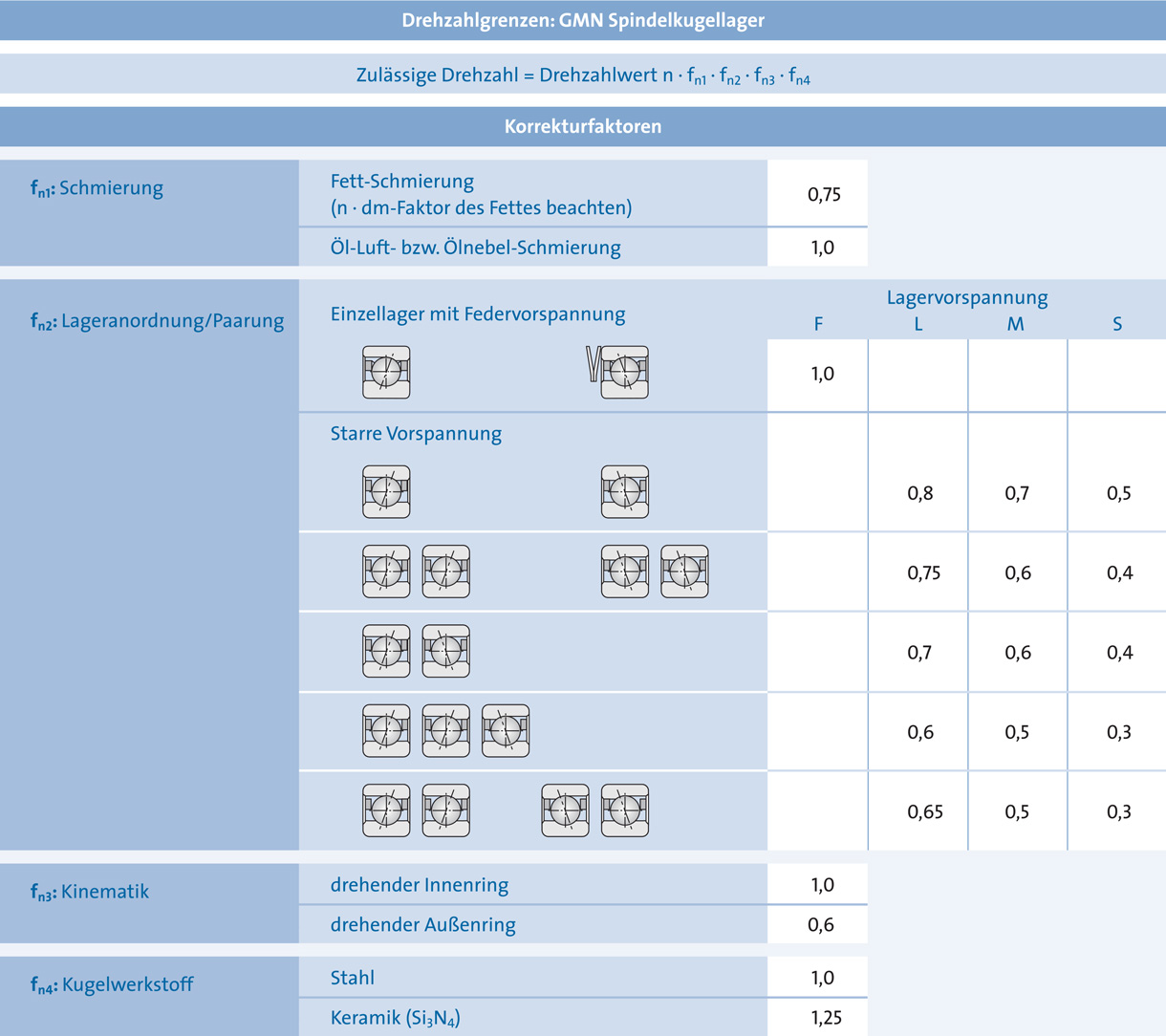
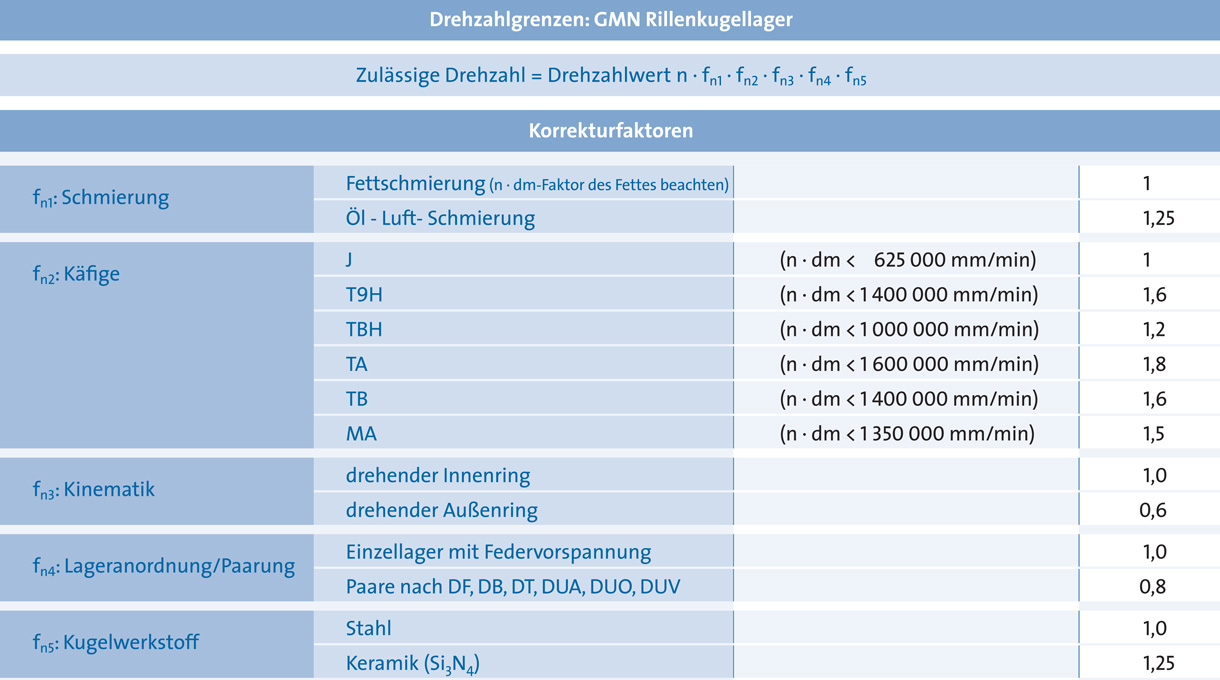
Die in den Lagertabellen angegebenen Drehzahlwerte sind nominelle Grenzdrehzahlen, die sich auf ein mit Federn vorgespanntes Einzellager unter durchschnittlichen Bedingungen beziehen. Dies sind:
Weichen die Betriebsverhältnisse von den genannten Bedingungen ab, dann sind Korrekturfaktoren zu berücksichtigen (Korrekturfaktoren und Drehzahlwerte sind Richtwerte).
Das Technische Informationsblatt „Drehzahlgrenzen für Spindelkugellager“ finden Sie hier oder im Downloadbereich.
Bei Fragen zu Ihrer speziellen Anwendung stehen wir Ihnen mit unserer langjährigen Erfahrung gern zur Verfügung.
Eine ausreichende statische Tragfähigkeit sichert die materialbedingte Formstabilität der Lagerkomponenten unter höchstmöglichen Krafteinflüssen im Betriebszustand. Insbesondere bei Maschinenstillstand (Werkzeugwechsel) und extrem
langsamer Rotationsbewegung können hohe mechanische Belastungen auftreten.
Die statische Tragfähigkeit (statische Kennzahl fs) wird unter Berücksichtigung von Lagereigenschaften und Betriebsbedingungen ermittelt.
Ist die statische Kennzahl fs größer als 2,5, ist eine ausreichende statische Tragfähigkeit des Lagers gewährleistet (keine plastische Verformung der Berührungsstelle Kugeln/Laufbahnen).
Statische Kennzahl fS
fs = i · C0 / P0
i: Anzahl der Kugellager
C0: statische Tragzahl [N]
P0: statisch äquivalente Belastung [N]
Die statisch äquivalente Lagerbelastung P0 bezeichnet einen Richtwert, der verschiedene Betriebsbedingungen und Belastungsverhältnisse vereinheitlicht und für die Berechnung der statischen Kennzahl fs berücksichtigt.
Statisch äquivalente Belastung P0 [N]
P0 = X0 · Fr + Y0 · Fa [N]
wenn P0 < Fr , dann P0 = Fr
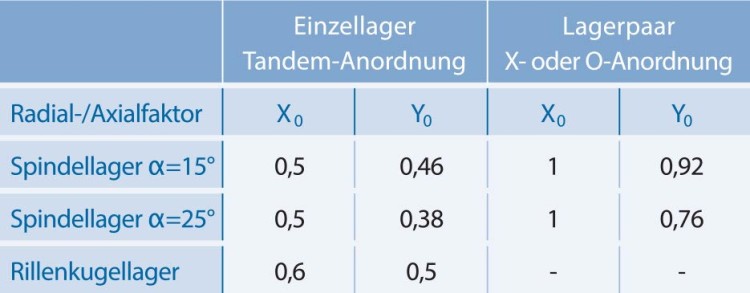
X0: Radialfaktor
Y0: Axialfaktor
Fr: Radialkraft [N]
Fa: Axialkraft [N]
Die Abhängigkeit der Lagerstabilität von Lagerart, Berührungswinkel und Lageranordnung wird mit Radial-/Axialfaktoren einkalkuliert.