RPM and load carrying capacity are decisive factors in calculating the performance of ball bearings.
GMN develops ball bearings for the highest RPMs and maximum loads, in order to optimize efficiency and machine life expectancies. The RPM limit is a decisive dimension for bearings. In the area of the contact surfaces between the ball and the rings, running friction and therefore bearing temperature increases with an increase in RPMs.
The friction produced in the bearing is decisively influenced by:
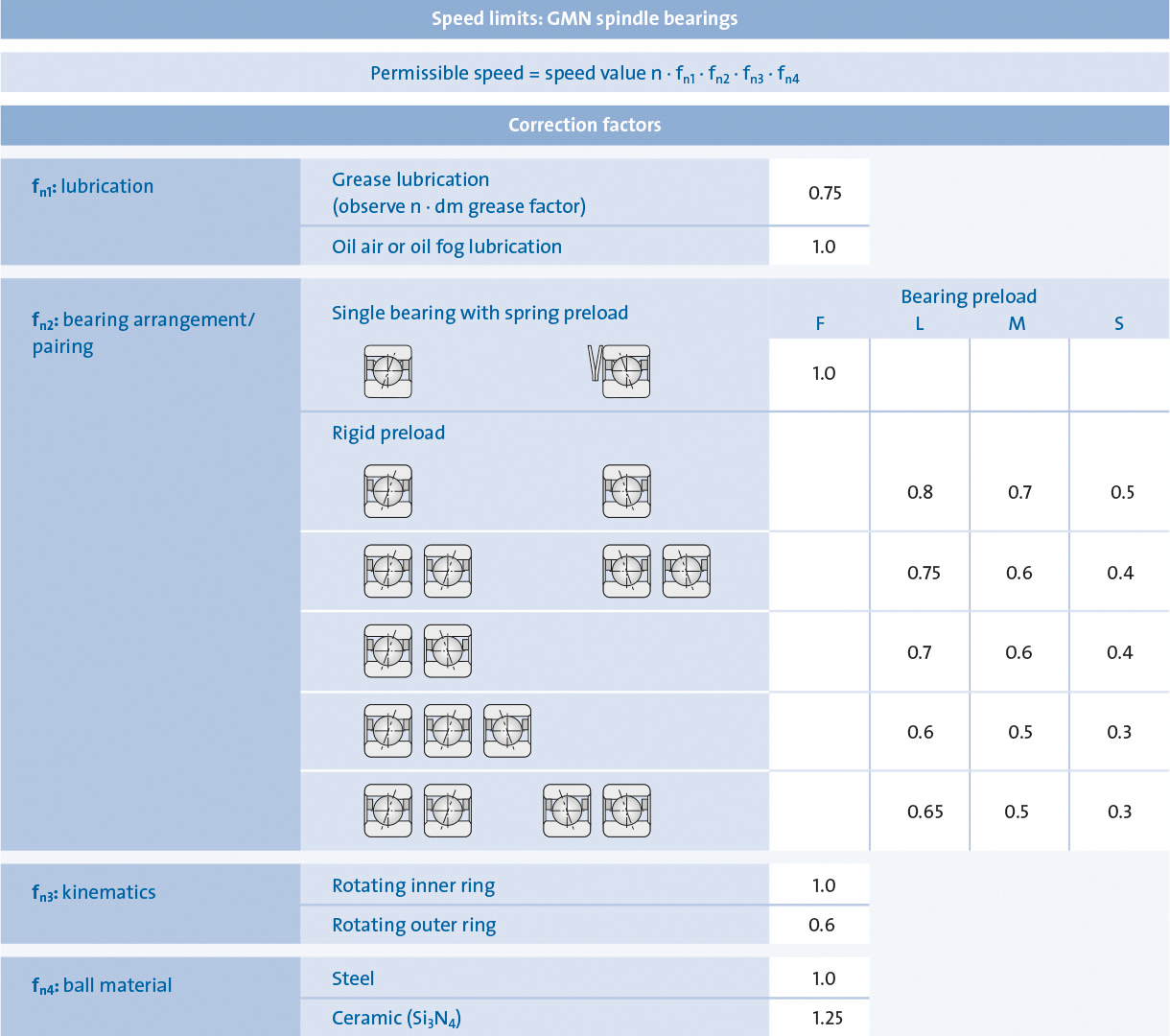
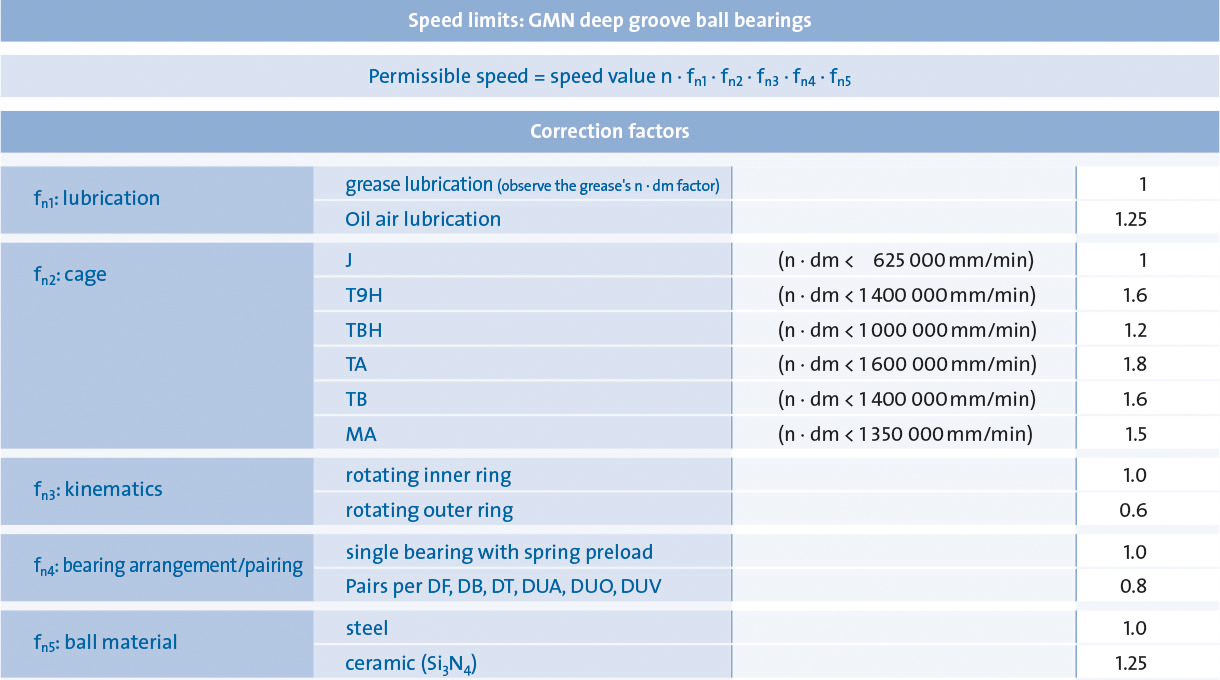
The RPMs shown in the bearing tables are nominal limiting speeds, which are related to individual bearings that are pre-stressed with springs or under average conditions. These are:
If the operating conditions deviate from the stated conditions, correction factors must be taken into account (Correction factors and speed values are guide values).
The technical information sheet “Speed limits for spindle ball bearings” can be found here or in the download area.
If you have questions about a special application, we would be happy to contribute our many years of experience into your project.
Sufficient static load-carrying capability secures material-related shape stability of ball bearing components under the highest-possible force influences in operationg mode. Especially when the machine is stopped (for a tool change) or rotational movement is extremely slow, high mechanical loads can occur.
Static load-bearing capacity (fS static index) is determined using bearing properties and operating conditions.
If the static fS is greater than 2.5, sufficient load-carrying capacity of the bearing is assured (no plastic deformation of the ballandgroove contact points).
Static key figure fS
fs = i · C0 / P0
i: Number of ball bearings
C0 : static load rating [N]
P0 : statically equivalent load [N]
Statically equivalent bearing loads (P0) refer to a guidance value which brings together various operating conditions and load ratios, and is used for calculating key static figures.
Statically equivalent load P0 [N]
P0 = X0 · Fr + Y0 · Fa [N]
if P0 < Fr then P0 = Fr
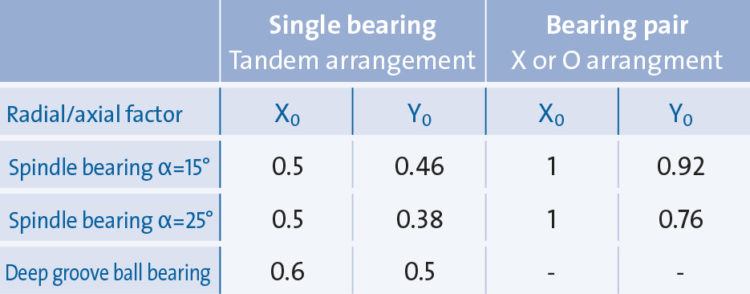
X0 : Radial factor
Y0 : Axial factor
Fr : Radial force [N]
Fa : Axial force [N]
The dependency of bearing stability for type of bearing, impact angle and bearing arrangement is computed with radial and axial factors.